In order to evaluate and understand issues that can be associated with vignetting (the blocking of rays that pass through the outer edges of an imaging lens), roll-off and relative illumination, sensor sizes, and formats need to be considered. In addition to the following overview, more information on sensors and formats can be found in Understanding Camera Sensors for Machine Vision Applications.
Figure 1: Roll-Off is the Decrease in Relative Illumination with Respect to Field that is not caused by Vignetting, but by Radiometric Laws
Matching Sensors with Lenses
One issue that often arises is the ability of an imaging lens to support certain sensor sizes. If the sensor is too large for the lens design, the resulting image may appear to fade away and degrade towards the edges; this effect is caused by vignetting. As the resolution demands of a system increase, one of two things needs to happen: pixels need to get smaller or sensors need to get bigger. As is detailed in the sections on MTF and Diffraction Limit, continuous reduction in pixel size produces significant issues regarding the optics’ ability to resolve true detail. This concern, combined with the signal to noise and sensitivity issues associated with current sensor technology, results in sensors having to grow in size; such growth causes these issues regarding vignetting and roll-off, unless the proper lens is used.
Relative Illumination
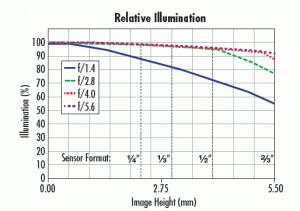
Relative Illumination is a way of representing the combined effect of vignetting and roll-off in an imaging lens, and is generally given as a percentage of illumination at any point on the sensor normalized to the position in the field with maximum illumination. Vignetting and roll-off are two separate components of relative illumination. An example of RI is shown in Figure 2. More details on how to read this curve can be found in Lens Performance Curves
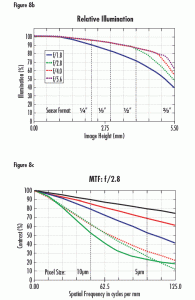
The curve in Figure 2 shows that at its lowest aperture setting (f/1.4 – the blue line), this lens has an RI of 57% of the illumination level of the image center at the corner of a 2/3″ sensor. Under the same conditions, the lens has an RI of 72% in the corner of a ½” sensor. As the sensor gets smaller, the RI improves. Also note that the RI improves as the f/# is increased; this occurs until there is no more vignetting in the lens, at which point all higher f/# settings will have the same illumination profile. Increasing the f/# generally does not increase the image circle size much, in that a lens designed for a particular sensor size will not perform well on a larger sensor even with the f/# stopped down.
Roll-off will still occur when the lens is stopped down, as that is related to the angle of the rays and not the number of rays that pass through the lens. Many lenses will have an illumination profile that is highest in the middle of the field and is either flat or declines to some lower percentage as it approaches the edge. There are rare cases where the RI increases slightly across the image circle, but this is related to pupil compression and will not be covered in this text.
Vignetting Within a Lens 
Vignetting is the result of light rays not making it through the entire lens system to the sensor, due to being blocked by the edges of individual lens elements or mechanical stops. This clipping of rays can be intentional or unintentional, and in some case is unavoidable. Vignetting is most often seen at or in lower f/#s, short focal length lenses, or lenses where higher resolutions need to be achieved at a lower cost.
Figure 3 demonstrates clipping as it may occur for the same 16mm lens at different f/#s (f/1.8 and f/4). Note the clipping of rays in Figure 3a, as indicated with red circles; these rays are not able to pass through the all of the optics in the lens. Figure 3b, on the other hand, demonstrates an example without vignetting. The vignetting in Figure 3a could have several causes, including diameter limitations of the optics or a need to eliminate the rays to block stray light. Vignetting is sometimes purposely included in a lens design to improve overall lens performance or reduce cost.
Figure 3: A 16mm Lens Design at f/1.8 (a) and f/4 (b). At f/1.8 vignetting occurs where light rays are clipped by the edges of the lens
Vignetting to Gain Performance (Selective Vignetting) 
Vignetting is often used to maximize the resolution of a lens design across the entire image circle. Since it is more difficult to direct the rays that create the edge of an image to the desired location on a sensor, higher resolution objects are generally more difficult to reproduce at the edge of the image than at the center. Rays that end up on the wrong pixel will degrade the image at that location; one way to manage this is to eliminate these rays from the system. If the undesired rays do not make it to the sensor, they cannot degrade the image. Removing these mis-directed rays, however, reduces relative illumination.
Effects of Vignetting at the Pixel Level: Large Pixels
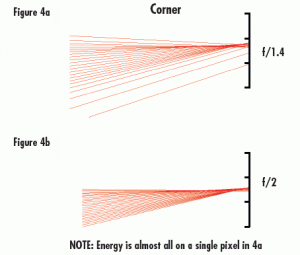
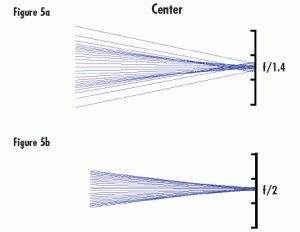
Figure 4 Illustrates light rays incident on a pixel in the corner of a sensor at f/1.4 (a) and f/2 (b). In Figure 4a, some light spills onto the adjacent pixel creating image and contrast degradation. Increasing the f/# (Figure 4b) essentially creates vignetting which clips those extraneous rays. Figure 5 illustrates this same vignetting effect at the center of the sensor. However, with these large pixels, the change in f/# has little effect on the overall image quality.
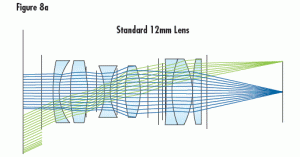
Vignetting can also be purposefully designed into lenses in scenarios in which the effects from manufacturing tolerances adversely affect the control of rays, causing image degradation. The looser the tolerances on the lens, the more adverse these degrading effects can become, and tightening the tolerances is often not practical due to the increase in manufacturing cost. Often, a balance must be struck between reducing manufacturing cost and maintaining image quality. In cases where cost is a primary factor, vignetting must be utilized in an attempt maintain resolution across the field of view. Doing such will have an adverse effect on the illumination profile. Designing vignetting into a lens can be accomplished in a couple different ways: by purposefully designing the clear apertures of the individual lens elements such that they vignette severely off-axis rays, or by introducing mechanical apertures to block aberrated rays, as shown in Figure 8a.
Effects of Vignetting at the Pixel Level: Small Pixels
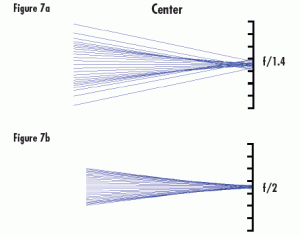
In Figures 6 and 7, the pixels have been reduced to half the size, yielding a 4X resolution increase. In this example, vignetting by increasing f/# greatly, improves performance across the entire sensor, as opposed to the first example which only slightly improved the imaging performance in the corner of the image. All of these Figures (4 – 7) exhibit nominal design capabilities and do not account for reduced performance that results from manufacturing tolerances. With tolerances included, the need for vignetting can be even more pronounced, especially in cases where cost is a driving factor.
Figure 4: Light Rays incident on Pixels in the Corner of a Sensor at f/1.4 (a) and f/2 (b). Increasing the f/# creates vignetting which clips the extraneous rays spilling onto the adjacent pixel in 4a
Figure 5: Light Rays incident on Pixels in the Center of an Image at f/1.4 (a) and f/2 (b). Increasing the f/# has no effect significant on image quality as all rays were contained in the desired pixel for each example
Figure 6: Light Rays incident on Pixels in the Corner of a Sensor at f/1.4 (a) and f/2 (b). Increasing the f/# creates vignetting which clips the extraneous rays spilling adjacent pixels
Figure 7: Light Rays incident on Pixels in the Center of an Image at f/1.4 (a) and f/2 (b). Increasing the f/# creates vignetting which prevents the extraneous rays from spilling onto nearby pixels
Demonstration of Vignetting in Different Lens Designs 
Figure 8 features a standard 12mm Lens design layout, along with both its relative illumination and MTF curves. Note the size difference of the ray bundles in 8a at the center (blue lines) and corner (green lines); the size difference demonstrates a large amount of selective vignetting. The vignetting leads to lower illumination at the edges of the image than in the center (8b). This is done in an effort to minimize the costs associated with materials and manufacturing tolerances, while maintaining reasonable performance at a lower price.
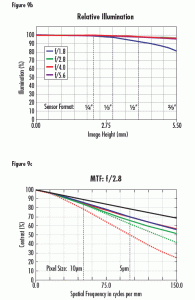
The lens in Figure 9, an ultra-high resolution 12mm lens design, has a much more evenly sized ray bundles across the field (9a) due to a low level of vignetting. This translates to much more even relative illumination across the entire sensor (9b). The lens in this example is designed using more costly materials at tighter tolerances, which allows it to maintain high levels of performance across the image, without the need to introduce vignetting to improve its performance. The trade off in using such a lens is that the ultra-high resolution lens is more expensive than the standard design.
Figure 9: A Ultra-High Resolution 12mm Lens Ray Path (a), Relative Illumination Curve (b), and MTF Curve (c)
Illumination Roll-Off 
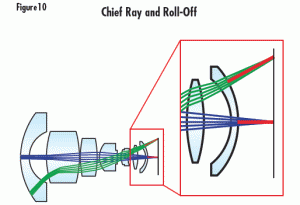
In its simplest form, the maximum brightness of a lens for some given image circle with no vignetting is limited by the fourth power of the cosine of the chief ray angle in image space. This is known as cos4q rolloff. Figure 10 shows the chief rays for the center and the corner of the image (highlighted in red).
Figure 10: Imaging Lens Layout, Highlighting the Chief Rays of the Ray Bundles Belonging to the Center (blue lines) and the Corner (green lines) of the Image. These define the angle which is used to approximate roll-off
In many applications, roll-off is not an issue, but it can be problematic when the chief ray angle becomes quite steep. This is especially true in applications utilizing large sensors, line-scan applications, and wide angular FOV (short focal length) applications. Table 1 shows how roll-off increases with angle. Notice that for an angle of 15°, there is a reduction in relative illumination of about 13% from the center to the corner, but by doubling the angle, the roll-off increases to nearly a 44% reduction of RI. Roll-off must be considered in applications with short working distances and large fields of view. This can produce large chief ray angles in image space, regardless of sensor size.
One way to correct for roll-off is by designing the lens to be image space telecentric. In doing this, the difference in the angle of the chief rays will be 0°, which produces even illumination. Another way to offset roll-off is to create unbalanced illumination on the object under inspection. By mounting additional lights closer to the edges of the object under inspection or by adding an apodizing neutral density filter onto the lens, roll off-can be mitigated.
| Difference in Chief Ray Angle | Maximum Relative Illumination Level Center to Corner |
|---|---|
| 5° | 98.5% |
| 10° | 94.0% |
| 15° | 87.1% |
| 30° | 56.3% |
| 45° | 25.0% |
| 60° | 6.3% |
Table 1: Relation between chief ray angle and relative illumination at the corner of an image, assuming 100% relative illumination at the center.
Roll-Off and Micro Lenses 
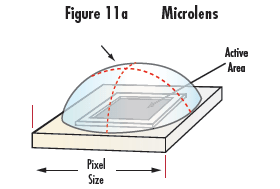
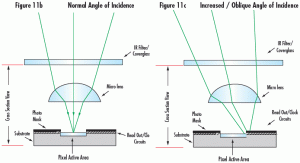
Micro lenses are utilized on many sensors in an effort to increase the amount of light making it to the active pixel area. Like all other lenses, micro lenses have an angular acceptance in which they operate most efficiently. As the angle of incidence increases, the amount of light that makes it to the active area of the pixel is reduced. Most lens designs attempt to keep their image space chief ray angles below 5 to 7° in order to reduce these effects. Figure 11a shows a micro lens over the pixel. Figures 11b and 11c show how light is focused at normal incidence and at an oblique incidence to the micro lens, respectively. Normal incidence would represent the center pixel on the sensor. At this position all rays are focused onto the active area of the pixel. At oblique angles, not all rays make it to the active pixel area. This results in additional reduced relative illumination beyond what is specified in a lens’s relative illumination curve.
Was this helpful?
4 / 0