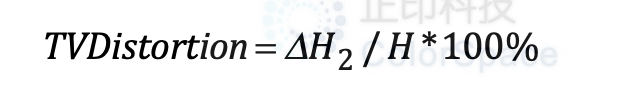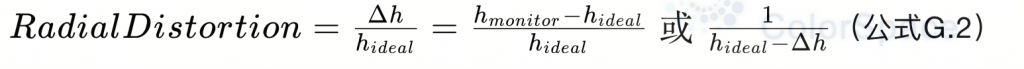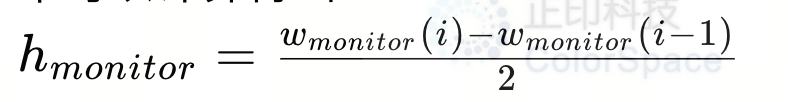发布时间:2024年4月12日
01 | 定义解读: Geometric Distortion
相对于监视器上的直线投影,图像的失真应最小化。
G.1 概述
本附录提供了不同畸变定义及其测量方法的基本信息。畸变是与理想情况的偏差量,畸变的定义取决于什么被认为是理想情况。出于实际原因,这里描述了两种主要的畸变定义:电视(或画面高度)畸变和相对于直角投影的几何径向畸变。”电视畸变”是一个参考的单一值,广泛用作显示在电视系统上可观察到的外边缘长线弯曲程度的实用方法,而”几何畸变”则是根据图像径向高度或入射角给出的变体函数,它提供了系统更精确的局部物理特征。
请注意,本子条款中使用的”图像径向高度”(小写”h”)指的是从图像中心到径向方向的图像距离,应与”画面高度”或”图像高度”(大写”H”)区分开来。
02 | ISO 16505:2015标准的附录G部分,主要讨论了车辆用摄像头监控系统(Camera Monitor Systems, CMS)的畸变测量方法和要求:
G.2 电视畸变
电视畸变是一个单点比率,用来指示矩形图像区域最外层长线的曲率程度。如果显示器以横向更宽的全景视图布局定位,则测量最外层水平线在其正交垂直方向上的曲率偏差量,位于角落处。
“电视畸变”(也称为”画面高度畸变(PHD)”)定义为:
其中:
- H 是显示器上显示的图像从底部到顶部的画面高度,位于图像水平中心的垂直线上;
- ΔH 是图像对角线角落处的垂直偏差量。
如果显示器以纵向更宽的纵向视图布局定位,则测量最外层垂直线在其正交水平方向上的曲率偏差量,位于角落处,并且可测量值等同于在90度旋转条件下的评估。
其中:
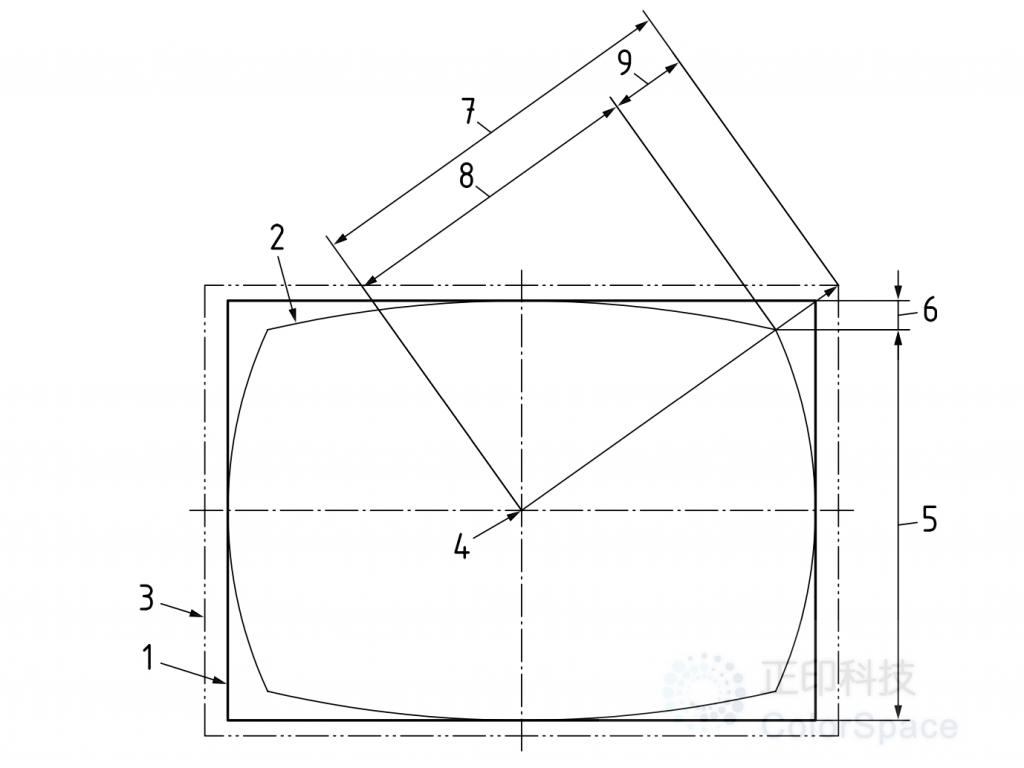
1. 车辆监控系统(CMS)显示器上实际显示的图像区域
2. 物体空间中场景矩形区域的投影,其线条是显示器上显示的最外层连续线条,带有畸变
3. 场景矩形区域的理想直角投影图像,其在显示器上的实际投影图像切于显示器的最外层边界线(见线2的点)
4. 图像中心
5. H:图像水平中心处显示器上的输出图像垂直高度
6. ΔH:图像最外层连续线条的垂直偏差(线2和3的角点之间)
7. h:理想直角投影下的图像径向高度(距离光学中心轴)
8. hideal:显示器上带有畸变的图像实际径向高度
9. Δh:图像径向高度偏离理想直角投影的程度
请注意,这个值受到显示视场量的影响,因此应与显示视场、纵横比或放大纵横比一起考虑。由于CMS功能显示区域的输出图像格式不局限于具有确定纵横比的传统电视系统,如4:3或16:9,因此在CMS上测量的电视畸变值应明确提及测量的纵横比。否则明确提及,电视畸变应在纵横比为4:3的条件的角落点测量,并且应报告相应的测量点。
其中:
1. 车辆监控系统(CMS)显示器上实际显示的图像区域
关键点
2. 投影在显示器矩形最外层四个角点内的矩形场景图像(见点11)
3. 当无畸变时,内嵌于矩形场景2的理想图像
4. 显示器上的虚构投影图像,为覆盖显示器最外层线的矩形区域,在点9和10处(这些线条在CMS显示的图像内不可见,因为线条已经畸变到了显示器图像区域外)
5. 图像中心
6. H : 显示器上图像水平中心处的输出图像垂直高度
7. ΔH:目标场景最外层水平线在角落处的垂直偏差量,其线条在点9处与显示器最外层边界线相切(此点在CMS输出图像内不可见,因此只有在光学中间图像可访问时才能测量)
8. ΔH:穿过图像角落点11的场景水平线的垂直偏差量
9. 显示器最外层水平边界线与最外层水平线的切点,是CMS显示器内唯一可观察到的点
10. 显示器最外层垂直边界线与最外层垂直线的切点,也是CMS显示器内唯一可观察到的点
11. 显示器的角落点和内嵌矩形的交叉点
12. 由线4描述的矩形的虚构边界线的交叉点
对于桶形畸变,它是负数,对于枕形畸变,它是正数。因此,电视畸变是一个显示明显畸变量的单一代表性值。换句话说,电视畸变指的是在评估全景布局时,较长尺寸角落点向垂直方向弯曲/偏差的量。
使用该定义是因为阴极射线管上的输出显示图像可能表现出枕形失真。 然而,CMS系统中的电视畸变需要以自洽的方式进行测量,即利用显示在监视器上的捕获图像进行测量。在当今大多数平板显示器(FPD)中,监视器是一个绝对的矩形。 因此,枕式电视失真计算如下:
其中:
H是水平中心处的最大图像高度。
G.3 几何径向畸变
几何径向畸变是相对于理想直角投影的偏差比率。在直角图像投影中,3D实际物体世界中的直线将被投影到2D图像平面上,形成一条直线。这个定义下的理想情况通常被称为无畸变投影,或理想的针孔投影。这里描述的几何径向畸变是相对于这种理想直角投影的偏差比率。
对称镜头的几何径向畸变计算类似于放大倍率测量。几何径向畸变是图像径向高度Δh与理想直角镜头中预期图像径向高度hideal的比率:
其中:
- hmonitor 是观察到的图像径向高度;
- hideal 是从光学轴心点出发的非可观测理论图像径向高度。
为了获得畸变曲线,应从测量中获取理想投影的投影图像径向高度hmonitor和hideal。从棋盘图测量中可以计算得出:
其中icentre是棋盘图的估计中心,其中光学轴可以找到。通常,相机系统的光学轴心与图像中心对齐,因此假设图像中心是光学中心。这里使用的wmonitor的1/2因子仅用于保持7.5.2中使用的描述的一致性,在该描述中,图像径向高度被描述为最小放大倍率计算的1/2 * wmonitor。
hideal 是捕获图像上的非可观测点,其高度应首先从测量曲线中估计。在理想直角镜头中,垂直于光学轴的平面表面上的图像在整个图像上展示恒定的放大倍率,并且图像径向高度将根据从光学轴(中心)的偏移距离线性增加。
畸变参考了从光学轴以直角投影展开的理想图像径向高度。本子条款提供了计算和数据处理程序,以获得CMS镜头系统的畸变特性。为了获得整个图像区域的畸变特性,畸变特性是沿着整个对角线方向测量的,而不是沿着中心水平线测量的。但下面给出的示例是针对水平线的测量描述的。
测量畸变曲线的步骤
下面的过程描述了获得与理想直线透镜系统相应的畸变曲线的步骤:
a)捕获棋盘图卡图像并测量投影在监视器上的每个图卡方格的位置1/2 * wmonitor(i),其中i是图卡的第i步。 有关摄像机轴垂直于图卡方向的详细说明,请遵循附录C中给出的说明。
b) 假设测量数据中的光学中心,并将预期中心点参数化为icentre。 如果估计的第i个图像中心点不合适,则应进行校正以使误差最小化,如步骤i)所示。 (根据图卡方块步长,所测量的i是离散步长,但是实际的icentre是实数,而不一定是离散整数值。 当图卡的方块中心不完全对准光轴中心时,它将是一个中间实数)
c)对于监视器上的每个测量的图卡正方形位置i,从估计的中心(icenter)计算距离(径向高度)),并绘图径向高度与图卡正方形边缘的关系。hmonitor=1/2*(w’monitor(i)-w’monitor(icenter)) , 它可以使用原始i位置绘制,但为了简化以下公式,应该使用新的移位水平轴j重新绘制,以使光轴到原点的距离j = 0,其中j = i- icentre。
d)从步骤c中的绘图中,根据所需精度获得三阶或五阶多项式插值曲线
例如hmonitor(j)= aj5+ bj4+cj3+dj2 +ej + f),并从插值的多项式曲线获得一阶微分曲线为dhmonitor(j)/dj,其分别给出dhmonitor(j)/ dj = 5aj4 + 4 bj 3 + 3cj 2 + 2dj +e。 高阶多项式插值可以提供一个更准确的近似从复杂的失真,但它可能会受到影响的风险,测量不准确。 对于复杂的畸变特性,仅在光轴附近应用插值,以获得计算直线投影的理想图像径向高度所需的dhmonitor(j)/ dj值。 该过程对应于用于计算理论理想直线投影的系统的轴向焦距的估计。
e) 在步骤d)中获得的多项式在光轴处的一阶微分提供了在理想直线情况下根据图表平方步长投影在监视器上的特征图像的增加比率。 理论图像径向高度通过乘以在图像中心处的斜率dhmonitor(j)/ dj值(dhmonitor(j)/ dj j= 0)来获得,该斜率在整个图像中是恒定的。对于具有j的直线系统的图像,它被给定为hideal(j)={dhmonitor(j)/ dj | j=0}*j
f) 根据下式将步骤c中的绘图的水平轴转换为理想的直线图像径向高度,根据步骤e的计算。 该绘图现在将在光学中心j = 0处呈现1:1的关系。
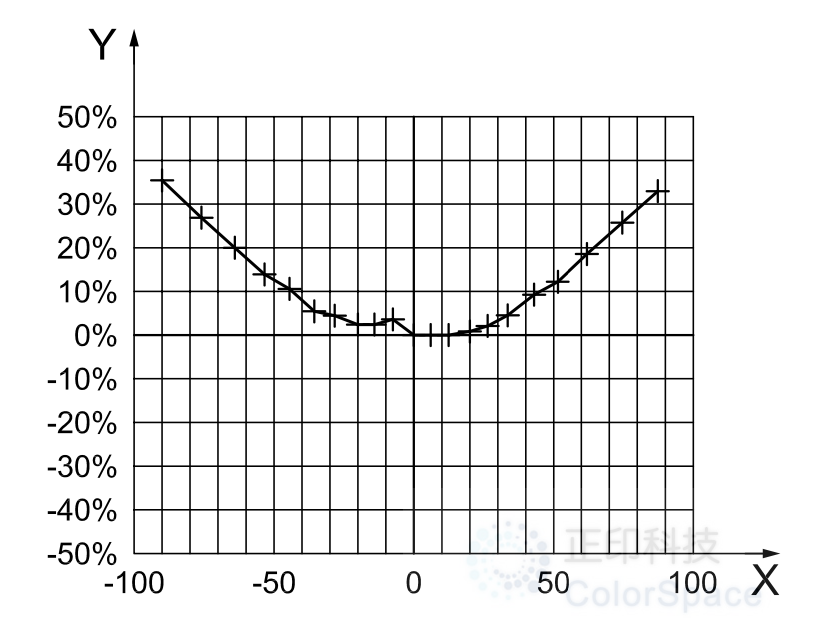
g)计算hmonitor(j)与理想直线参考距离hideal[j]之比,减去1,按式(G.2)求出几何径向畸变。
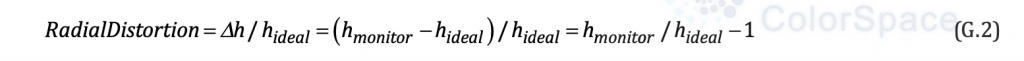
h)由于理想图像径向高度是在输出图像上不可直接观察到的理想直线投影的理论点,因此将水平轴与实际可观察的高度重新转换。见图 G.1 和图 G.2
i)在对称系统中,该畸变曲线应在光学中心对称。 由于在步骤b中对图像中心点的错误假设,绘制的数据可能出现不对称。 在这种情况下,重新调整参数化的中心点icentre,以最大限度地减少不对称性,并获得穿过中心点的平滑曲线。 如果调整得当,中心处的失真曲线将为零,并在图像中心点上连续。
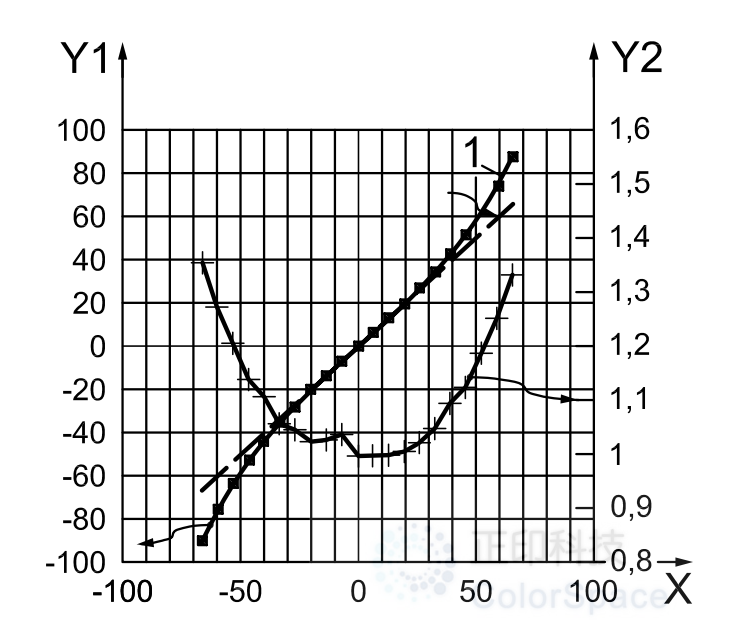
Y1:监视器图像上图卡正方形的位置[mm]
Y2 :1 +径向失真
1:理想图像位置对于直角投影(即无畸变投影,斜率为1的线条)
图G.4 -水平轴上的假设图像位置和测量的图卡距中心的距离
注:根据输出图像估计的光学中心应进行调整,以使上述曲线的不连续性最小化。 如果透镜设计仅在图像周边处表现出畸变,则中心不连续的影响将不会如此明显,并且畸变曲线的不对称性可能仅在图像的周边处变得可观察到。 如果外围的失真曲线表现出一定的不对称性,在这种情况下,调整估计的图像中心,使外围的失真曲线对称。 但是不对称的原因可能是CMS光学器件的倾斜组件,包括图像传感器装置的倾斜组件,导致CMS失真特性的固有不对称。
测试环境:
摄像头端:D65,6500K±1500K,>500lux
屏幕端:照度无要求,0~10lux
主要使用设备:图卡切换设备、LE007反射面光源、LE006灯箱、成像色度计、移动升降测试桌、图像测试卡等。
相关阅读:
联系我们:
如果您也对CMS的色彩还原相关测试感兴趣,或者您对CMS测试比较关注,欢迎与我们留言,也可邮件咨询: sales@colorspace.com.cn,分享您的看法或提出您的问题!

Was this helpful?
2 / 0