镜头（光学）畸变是一种像差，会导致图像边缘附近的直线弯曲。这对于建筑摄影和摄影测量（从图像中得出的测量结果）可能会带来麻烦。最简单的近似是三次方程，r u = r d + kr d 3 ，其中 r d 是畸变半径，r u 是未畸变半径。根据 k 的符号，它可以是“桶形”（如右图所示）或“枕形”。对于复杂镜头，可能会出现一种称为“胡须”畸变的混合情况，这种情况更适合用五次近似来描述（r u = r d + h 1 r d 3 + h 2 r d 5 ）。
镜头畸变及其校正系数在 Checkerboard 模块中计算，该模块计算三阶、五阶和正切/反正切畸变模型，以及锐度和若干其他因素。Dot Pattern 执行符合 CPIQ 标准的畸变测量。SFRplus 测量畸变的详细程度几乎与 Checkerboard 相当。SFRplus 的畸变结果体现在图像、几何、畸变、视场角和径向畸变图中。eSFR ISO 测量畸变的精度略低于 SFRplus。
失真在广角、长焦和变焦镜头中最为严重。对于近距离拍摄的图像，失真通常比远距离拍摄的图像更严重。它可以通过软件轻松校正。更多详情请参见失真：方法与模块。
相关标准：
- CPIQ 局部几何畸变
- ISO 17850 — 几何畸变（GD）测量
失真模块和方法
本页介绍了 Imatest 的畸变计算，比较了不同的畸变公式和模块。
失真公式 – 模块 – 电视失真与视野 – 图像、几何、失真、视野显示
径向畸变图 – 畸变等高线图 – 比较结果 – 链接
镜头畸变有两种基本形式，桶形和枕形，如下图所示。
 无畸变 |  桶形畸变 |  枕形畸变 | 除了这三种之外，还可能出现“胡须”或“波浪”畸变，即中心附近呈桶形而边缘附近呈枕形，或者相反。 |
失真公式
在适用于多个模块的方程中，r d 是归一化到中心到角落距离的失真（测量）半径。r u 是未失真的半径。r 归一化到中心到角落距离。
| N* | 畸变模型 | 标准 | 部门 （功率比标准型号少一） | 笔记 |
| 1 | 3 阶多项式 | 𝑟𝑢=𝑟𝑑+𝑘1𝑟3𝑑 | 𝑟𝑢=𝑟𝑑/(1+𝑘1𝑟2𝑑) | [1][A] |
| 2 | 5 阶多项式 | 𝑟𝑢=𝑟𝑑+𝑘1𝑟3𝑑+𝑘2𝑟5𝑑 | 𝑟𝑢=𝑟𝑑/(1+𝑘1𝑟2𝑑+𝑘2𝑟4𝑑) | [2] |
| 3 | 切线（用于桶形失真） | 𝑟𝑢=tan(10𝑝1𝑟𝑑)/(10𝑝1);𝑝1>0 | [1][A] | |
| 3 | 反正切（用于枕形失真） | 𝑟𝑢=arctan(10𝑝1𝑟𝑑)/(10𝑝1);𝑝1<0 | [1][A] | |
| 4 | 上述选择中最佳（三阶、五阶和反正切/正切） | |||
| 6 | 5 阶 ALL 多项式 | 𝑟𝑢=𝑟𝑑+𝑘1𝑟2𝑑+𝑘2𝑟3𝑑+𝑘3𝑟4𝑑+𝑘4𝑟5𝑑 | 𝑟𝑢=𝑟𝑑/(1+𝑘1𝑟𝑑+𝑘2𝑟2𝑑+𝑘3𝑟3𝑑+𝑘4𝑟4𝑑) | [3] |
| 7 | 7 阶多项式和反正切/正切的最佳选择：可在 Checkerboard 中使用。 | |||
| 8 | 7 阶多项式 | 𝑟𝑢=𝑟𝑑+𝑘1𝑟3𝑑+𝑘2𝑟5𝑑+𝑘3𝑟7𝑑 | 𝑟𝑢=𝑟𝑑/(1+𝑘1𝑟2𝑑+𝑘2𝑟4𝑑+𝑘3𝑟6𝑑) | [4] |
| 9 | 7 阶 ALL 多项式 | 𝑟𝑢=𝑟𝑑+∑7𝑖=2𝑘𝑖−1𝑟𝑖𝑑 | 𝑟𝑢=𝑟𝑑/(∑6𝑖=1𝑘𝑖𝑟𝑖𝑑) | [4] |
| 10 | 9 阶多项式 | 𝑟𝑢=𝑟𝑑+𝑘1𝑟3𝑑+𝑘2𝑟5𝑑+𝑘3𝑟7𝑑+𝑘4𝑟9𝑑 | 𝑟𝑢=𝑟𝑑/(1+𝑘1𝑟2𝑑+𝑘2𝑟4𝑑+𝑘3𝑟6𝑑+𝑘4𝑟8𝑑) | [4] |
| 11 | 11 阶多项式 | 𝑟𝑢=𝑟𝑑+∑5𝑖=1𝑘𝑖𝑟2𝑖+1𝑑 | 𝑟𝑢=𝑟𝑑/(𝑟𝑑+∑5𝑖=1𝑘𝑖𝑟2𝑖𝑑) | [4] |
注：[1] 所有模块。[2] 除 eSFR ISO 外的所有模块。[3] 棋盘格和 SFRplus。[4] 仅棋盘格。
[A] arctan/tan 和三阶模型不足以测量波形（胡须）失真。至少需要五阶多项式。
棋盘畸变设置
标准（奇数系数）和除法（偶数系数）模型
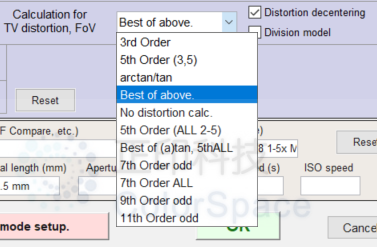
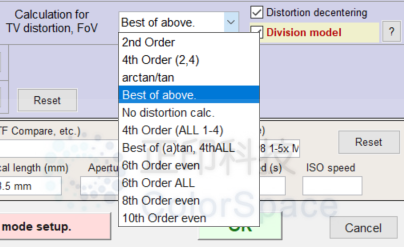
*N 是“更多设置”中畸变计算下拉菜单的索引。在上述模块的 ini 文件中，N = fovcalc。它由 INI 文件监视器显示。N = fovcalc = 5 表示不进行畸变（无 FoV）计算。4 表示 1-3 中的最佳值。7 表示 3 和 6 中的最佳值。
- 三阶方程是教科书中的塞德尔像差之一，这些像差是对透镜退化的低阶多项式近似。它仅适用于小量畸变。
- 除法畸变模型（针对多项式）在相同系数数量下似乎比标准模型略为准确。选择此模型时，如上所示，n 阶（奇数）多项式将被替换为(n-1)阶（偶数）多项式。
- 第五（及更高）阶系数能产生更精确的结果，尤其适用于“波浪”或“胡须”形畸变，这种畸变可能在图像中心附近呈现桶形，而在角落附近呈现枕形（或反之亦然）。
- 具有所有多项式系数的两种设置（5 阶 ALL 和 7 阶 ALL）使用直到最大值的所有系数，而不是交替系数（奇数或仅偶数，取决于模型）。我们尚未观察到这些设置有多大优势。
- 高阶多项式（七阶或更高；仅适用于棋盘格）应谨慎使用，因为结果可能变得不稳定，尤其是在图像的边缘部分。用于计算系数的图像应在图像边缘附近具有有效的角点，并且应有足够的行或列。
模块
| 模块 | 评论 | 优势 | 缺点 |
| Checkboard | 极其准确。推荐用于新项目。 | 快速（模式检测后）。极其准确（足以用于相机校准）。失真中心计算非常快，应始终选择。还计算 MTF 和 LCA。取景和对齐不关键。工作距离范围广。适用于强桶形失真图像。 | 仅适用于棋盘格图案。棋盘格检测可能较慢，但其余计算速度快。 |
| Dot | 基于 CPIQ 第 2 部分文档。 | CIPQ 和符合 ISO 标准。还可测量横向色差（LCA）。 | 对错位不宽容。速度较慢。我们可能会添加 Checkerboard 中使用的算法，这些算法更加灵活。 |
| SFRplus | 高度通用的模块，具有多种图像质量因素测量功能 | 快速且中等准确。还能计算 MTF、横向色差、色彩和色调响应。适用于预失真图表（对强桶形失真图像特别有用）。详情请参阅 SFRplus 失真和视场测量，特别是关于使用预失真图表的部分。 | 略逊于棋盘格。图像应在顶部和底部条带上下留有少量空白。这限制了工作距离的范围。 |
| Distortion 不建议用于新项目。 | Imatest 原始（旧版）用于计算畸变的模块。可能在未来的版本中弃用。 | 适用于网格图案、线条和边缘，以及棋盘图案。 | 通常对强烈桶形失真的图像效果不佳。比仅使用棋盘格的方法准确性低，仅测量失真（不包括 MTF 等）。网格图案可能难以处理，因为如果线条太细可能会丢失，而如果太粗则会失去精度。 |
| eSFR ISO | 有限畸变计算。无畸变中心。 | 失真度与其他结果一同计算。 | 有限失真公式。不适用于高阶多项式。 |
TV distortion和FOV(Field of View)
SMIA* TV 畸变是根据畸变模型方程（以及预畸变图表的畸变参数）计算的。[*SMIA 是现已失效的“移动成像架构标准”，由诺基亚和意法半导体于 2004 年发起。]
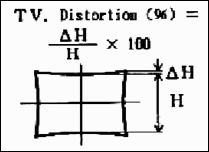
TV 畸变，源自 SMIA 规范，第 5.20 节。参照右侧图像，
SMIA TV 畸变 = 100( A-B )/B ; A = ( A 1 +A 2 )/2
右侧的框在 SMIA 规范中被描述为“几乎填满”图像。由于测试图表网格可能无法做到这一点，失真使用了一个高度为图像 98%的模拟框。请注意，符号与 k 1 和 p 1 相反。SMIA TV 失真 > 0 为枕形失真；< 0 为桶形失真。
算法：SMIA TV 失真并非实际从上下条带计算得出，这些条带的位置在不同图像中可能有很大变化。相反，它是通过使用所选方程及位于图像顶部下方和底部上方各 1%图像高度处的虚拟水平线，基于失真系数计算得出的。
 SMIA 与传统 (ISO) TV Distortion， SMIA TV distortion是传统TV畸变的两倍（2X），现已被纳入多项标准。右侧展示的传统定义改编自富士能发布的《光学术语》。相同的定义也出现在欧洲广播联盟（EBU）发布的《电影和电视摄像机镜头性能的测量与分析》中。 |
在 Imatest，我们传统上使用 SMIA 定义，因为它在移动成像行业中被广泛采用，且自洽。在传统定义中，TV 畸变是中心到顶部距离的变化（Δ）除以底部到顶部距离。在 SMIA 定义中，A 和 B 都是底部到顶部距离。
Imatest 5.1+ 允许您在传统的 TV 失真（现已成为包括 ISO 16505 在内的多项 ISO 标准的一部分）与 SMIA TV 失真之间进行选择。您可以在 Options II 窗口的左侧（Imatest 主窗口右下角的按钮）进行选择。该选择仅影响图形显示（ISO TV 失真 = SMIA TV 失真 ⁄ 2）。两种结果均包含在 CSV 和 JSON 结果中（适用于所有计算失真的模块）。
视场角（FoV）通过将畸变模型方程应用于图像的顶部、侧面和对角线（始终 r = 1）来计算 SFRplus、Checkerboard 和 eSFR ISO 的 FoV。为了以距离单位（厘米）计算 FoV，必须在 Rescharts 更多设置窗口中输入图表的几何距离。
| 模块 | 值 |
| SFRplus | Bar-to-bar chart height in cm |
| 棋盘 | 方形间距（厘米） |
| eSFR ISO | 注册标记垂直间距 cm |
如果输入镜头到图表的距离（以厘米为单位），还将计算角度视场（FoV）。
图像、几何、畸变、视场显示
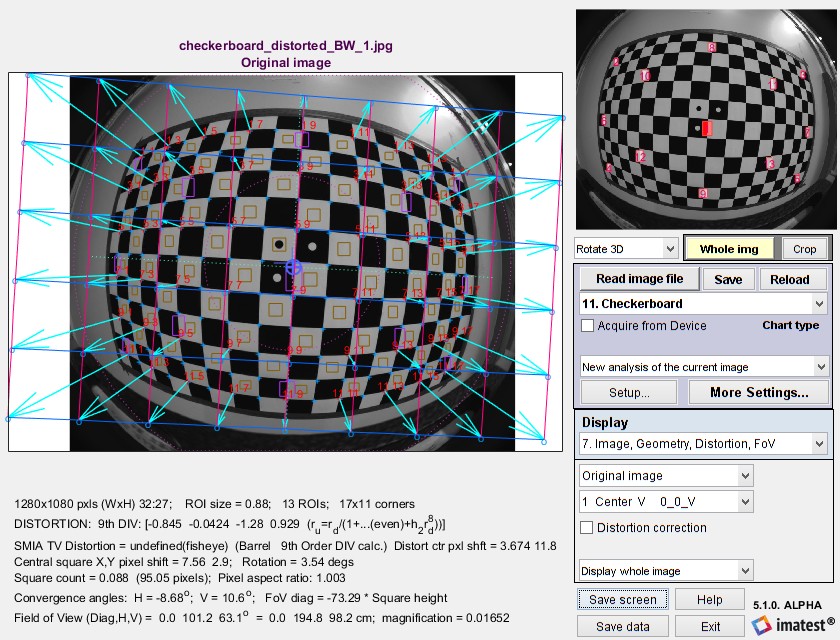
大多数计算失真的模块中都提供图像显示功能。在 Rescharts 中，它包含了大量信息（并非全部与失真相关）。以下是一个示例，展示了指向校正图像的箭头和线条，仅适用于棋盘格。（箭头和线条可以在“更多设置”窗口中开启或关闭。）
图像、几何显示展示箭头和校正后的图像位置
修正后的图像显示箭头指向原始图像
这是校正后的图像示例，还显示了箭头和线条。
此显示包含
- 尺寸和 ROI 信息（用于 MTF 计算）
- 畸变系数（此处为 9 阶分割模型）
- SMIA TV 失真
- 畸变中心偏移（以像素为单位）
- 图像（中心广场）移位
- 视野（对角线、水平和垂直；如果已输入适当的设置，则以度和厘米为单位）
- 收敛角度（透视畸变）
径向畸变图
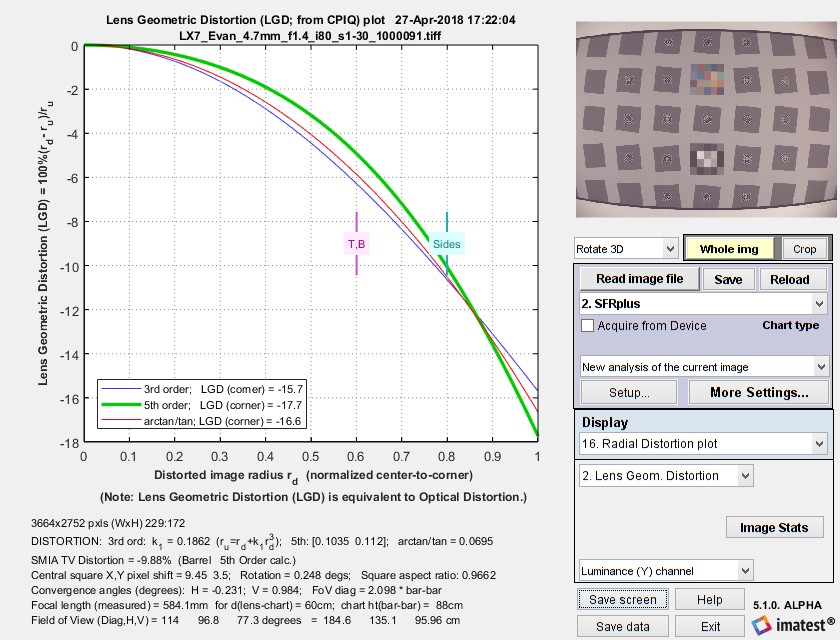
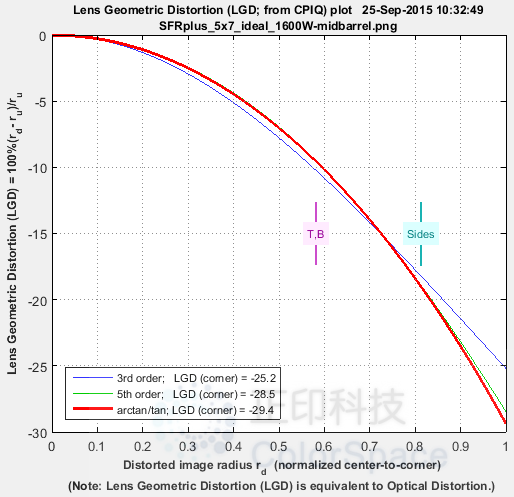
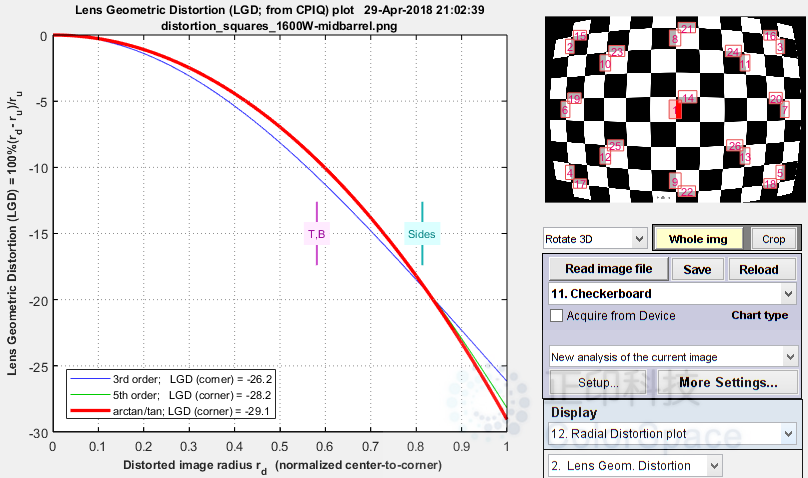
径向畸变图可在计算畸变的模块中使用。该图有四种显示选项：1. Delta-r，或 2. 镜头几何畸变（LGD），3. 未畸变的 r（r u ），或 d(LGD)/d(r u )。LGD 如下所示。
SFRplus 径向畸变图显示镜头几何畸变 100% ( r d – r u )/r u
显示选项为
- 半径变化Δr（归一化为中心到角落的距离，即半对角线）作为失真（输入）半径 r d 的函数。
Δr = r(未失真) – r(失真) = r d – r u - 镜头几何畸变（LGD），包含在 CPIQ 第二阶段规范中，等同于光学畸变（由 Edmund Optics 定义）。
LGD = 100% ( rd – ru)/ru - 未失真半径, r u
- 曲率 d(LGD)/d(r u )。此曲率（Imatest 5.0 中的新功能）可能有助于确定由失真引起的视觉退化，该退化可能与最大值-最小值成比例。符号的变化可能是比五阶多项式符号变化（并非总是计算）更好的胡须（波浪）失真指标。
实线显示了校正公式的结果：r u = r d + k 1 r d 3 （三阶多项式；蓝色）；r u = r d + h 1 r d 3 + h 2 r d 5 （五阶多项式；绿色）；或 arctan/tan 方程（红色）。最佳拟合（本例中为五阶）以粗体显示。使用这些方程时，|Δr| 通常作为 r（失真）的函数增加，即它往往在图像角落附近最大。所选值（或误差最小的值，err）以粗体显示。
畸变轮廓图 – 仅棋盘格
2021.2 新增。在 Rescharts 斜边模块第 4 部分：失真轮廓图中描述。
不同模块的结果比较
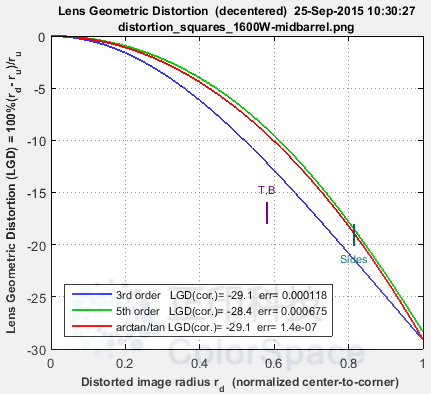
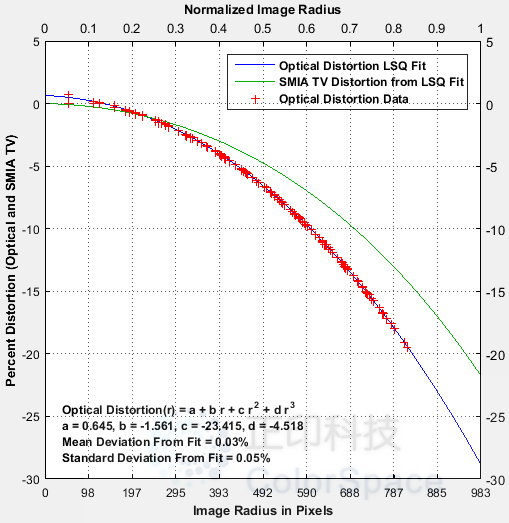
一组用于比较不同 Imatest 失真计算的图像可以通过点击 distortion_comparison_barrel_pin.zip 下载。这些图像由测试图表模块创建，转换为等大小的位图，然后进行同等程度的失真处理。如各模块的镜头几何失真图所示，一致性非常好。点阵图模块使用 Camera Phone Image Quality (CPIQ)规范中指定的算法，但其他模块产生的结果是等效的。
注：三阶计算（畸变和 SFRplus）不如五阶和 arctan/tan 计算准确（即，它们无法与实际畸变拟合得那么好）。点阵图中的绿线（SMIA TV 畸变）无法与其他图形进行比较。
Was this helpful?
0 / 0
