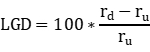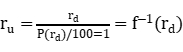发布时间：2023年8月4日

畸变校正

Imatest的测试卡和软件允许您测量成像系统的特性和参数。通常这些测量结果仅仅表明了系统性能和预期图像质量的极限。

但Imatest的一些结果可以通过校正测量的像差来提高图像质量-以及由同一系统拍摄的后续图像。无需购买新部件;不需要作出判断调用。它只需要一些数学和计算，你可以在我们自己的外部程序或Imatest模块中应用。这是图像处理流水线调谐的一个方面，其通常由设备中的专用图像信号处理（ISP）芯片来完成，以将原始传感器数据转换成适当的图像。

在Imatest，我们非正式地称之为“闭合循环”，因为它完成了从被测相机到测量，再回到相机的循环（以调整的形式）。

今天，我们将演示如何使用Imatest的径向失真测量来校正光学失真（无需购买新透镜）。

径向几何畸变

为了本文的目的，几何失真粗略地定义为图像中形状的扭曲，与相机真正遵循简单的针孔相机模型时这些形状的外观相比。（因此，我们在这里讨论的不是透视失真）。最明显的效果是场景中的直线变成图像中的曲线。

几何失真并不总是一件坏事-有时曲线镜头是为了艺术效果而特意选择的，或者使用广角镜头，失真被忽略，因为这是观众从这种情况下所期望的。然而，主观用户研究表明，日常图像的平均观看者在降低他们对图像质量的感知之前，他们愿意接受的失真量有限制。

对于需要精确校准的更多技术应用，例如计算机视觉中的3D空间中的点的定位，或者将多个图像拼接在一起以用于全景或沉浸式VR应用，也需要对失真进行表征（和校正）。

这种几何畸变几乎总是由于透镜设计，并且正因为如此（以及透镜是如何构造的），其通常被建模为（1）纯径向和（2）径向对称。

纯粹径向失真意味着，无论我们考虑一个点在图像场中的哪个位置，用于确定它经历的失真的该点的唯一相关方面是它离图像中心有多远。(For为了简单起见，在此我们将假设图像的中心是系统的光学中心，尽管通常这需要与径向失真一起测量或在径向失真之前测量。假设几何失真是径向的，对于降低表征它的问题的复杂性是非常有帮助的，因为代替二维上的二维向量场（每个像素位置处的X位移和y位移），我们只需要确定一维上的一维（每个半径处的径向位移）。

通过使用SFRPlus、棋盘格或点图案模块，Imatest可以从适当的测试图表的图像测量相机系统中的径向畸变。

Imatest中的畸变系数

Imatest可以返回两种不同类型径向失真的函数描述。两者都是由失真函数的多项式近似来描述的，但这两个多项式表示不同的东西。在许多情况下，它们在功能上是等价的，可以从一种形式函数转换为另一种形式函数。（为了简单起见，我们在这里忽略Imatest可以提供的tan/arctan近似，并且注意，当涉及到失真校正时，它可以以相同的方式应用，仅改变到前向映射步骤。）

在这篇文章的其余部分，我们将使用以下约定：

r_d是点的扭曲半径，即在观察到的（扭曲的）图像中它与中心的距离
r_u是点的未失真半径，即在未失真图像中出现的距中心的距离
r_d=f(r_u) 该函数称为正向变换，因为它采用未失真的半径值并将其转换为失真的半径。也就是说，它将透镜的畸变应用到该点。
r_u=f^-1(r_d) 该函数被称为逆变换，因为与正变换相反，它消除了透镜引入的失真。
P(·) 表示多项式函数

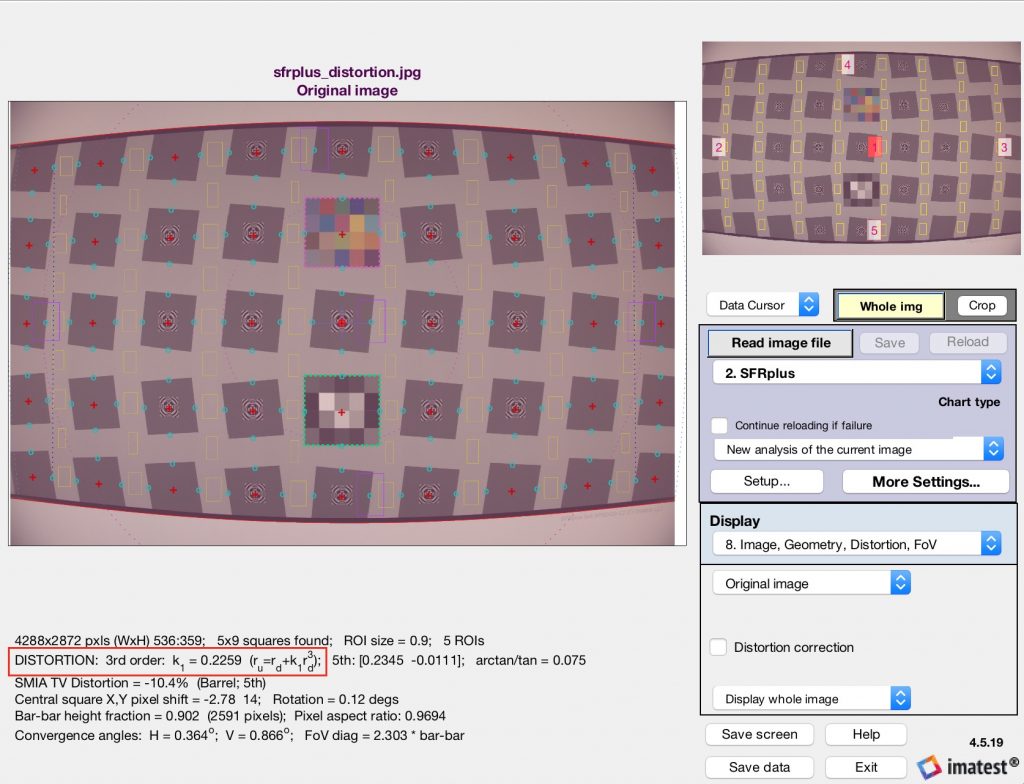
SFRPlus和棋盘模块返回描述校正失真的逆变换的多项式系数，r_u=f^-1(r_d) 在下面的Reschart中突出显示。

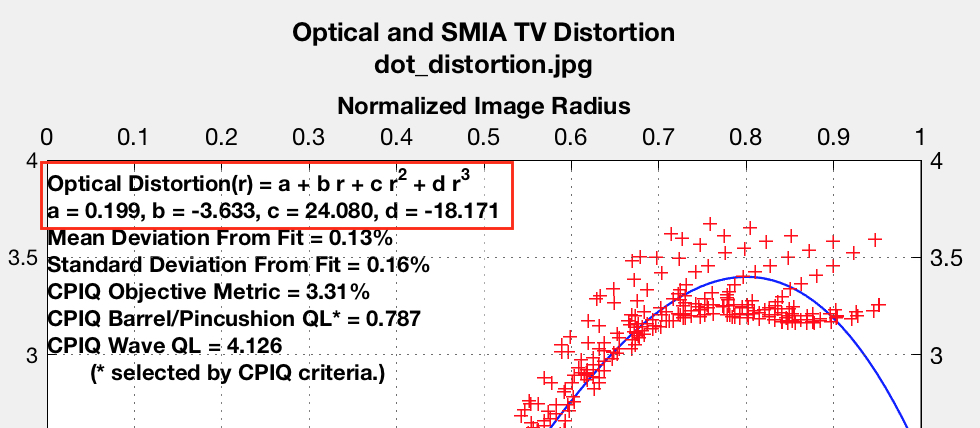
点图案模块返回径向失真的不同参数化的多项式系数，称为局部几何失真（LGD），有时称为光学失真。这是ISO 17850和CPIQ标准文件中使用的径向变形描述。

LGD被定义为相对于真实误差的径向误差，作为百分比（即，乘以100）：

通过将LGD视为畸变图像中半径的多项式函数，P(r_d) 我们可以重新排列该方程的边以产生更有用的方程，失真校正逆变换的有理多项式形式。因此，可以以与SFRPlus/棋盘结果相同的方式使用点图案结果（尽管在代码示例中，我们将直接将此有理多项式替换为正则多项式拟合近似）。

重采样失真校正

图像传感器的像素阵列基本上取落在其上的光的规则间隔样本的网格。然而，落在其上的光的图案已经被透镜扭曲，并且因此虽然传感器定期地对该光进行采样，但这些实际上不是光在进入透镜之前出现的规则样本。我们用于补救这一点的计算解决方案可以描述如下：

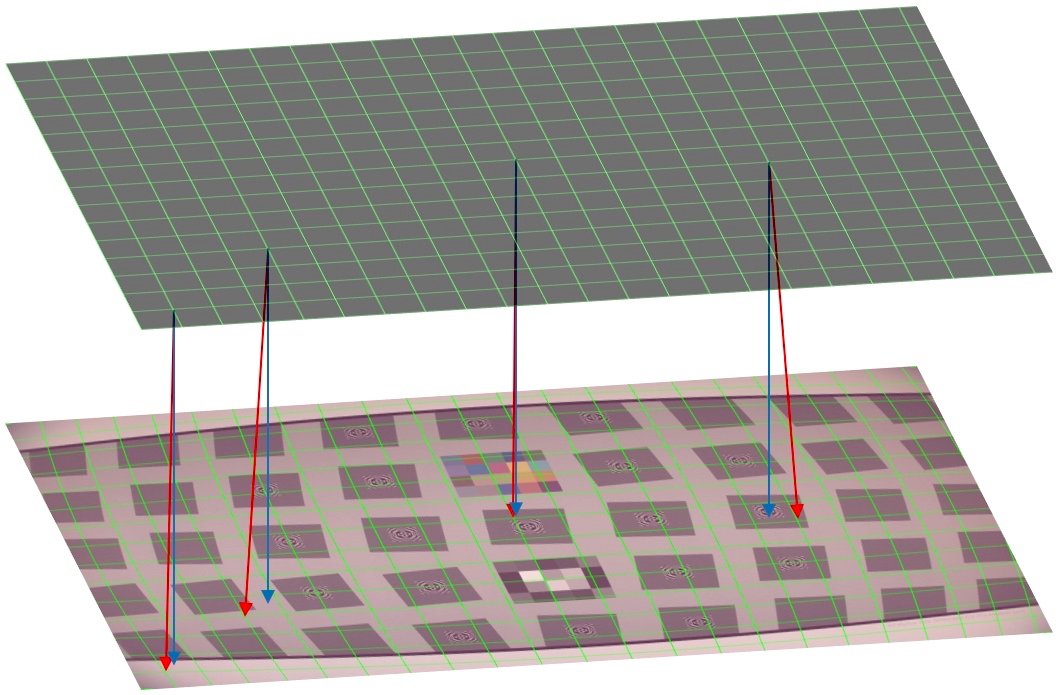
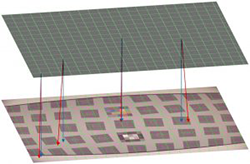
我们创建一个新的未失真的，规则间隔的网格（一个新的像素阵列）。在那些“虚拟传感器”像素位置中的每一个处，我们在该图像中传感器像素在不存在失真的情况下将投影的位置处从观察到的图像重新采样图像数据。因此，失真的图像由经历相同失真的网格重新采样，但是采样结果然后再次以规则间隔呈现-有效地消除失真。这一点在下面说明。

上方网格线的每个交点表示我们生成的未失真图像中的像素位置（我们的“虚拟传感器”中的像素位置）。显然，我们减少了这里的“像素”数量以增加易读性。图像的下半部分表示在网格以相同方式失真之后采样网格覆盖在其上的失真图像。上面的规则间隔的阵列位置将填充有从下面的失真图像不规则地采样的数据，如失真网格交叉位置所指示的。

作为进一步的视觉辅助，红色箭头从上部图像中的网格交叉点下降到下部图像中的相应网格交叉点。这些可以与蓝色箭头的结束位置形成对比，蓝色箭头指示如果未失真则像素样本将在那里。（显然，如果像素样本位置没有失真，即，使用蓝色箭头位置，则输出图像将从失真图像中有规律地采样，并且其本身将失真。）

一个例子

下面的MATLAB代码提供了如何进行这种重新采样的示例。你也可以在这篇文章的底部下载代码和示例图片。代码仅仅是一个特定的实现，但是-概念可以提取并应用于任何编程语言。

注意，在下文中，我们使用使用后缀‘_d’和‘_u’的惯例来识别分别与失真和未失真图像/坐标相关的变量，并且使用大写变量（诸如RHO）来识别与测试和输出图像相同大小的矩阵（将在下文中隐式地使用的属性）。

(0)将SFRPlus测试卡的图像加载到Imatest中并对其进行分析，以确定逆变换系数（此处显示在Rescharts交互模块中测量）。（或者，将图像加载到Dot Pattern模块中，并从那里检索LGD系数，并将它们转换为逆变换系数，然后沿着其余步骤。把这些输入MATLAB。

inverseCoeffs = [0.2259 0 1 0]; % distortion coefficients reported by SFRPlus
im_d = double(imread('sfrplus_distortion.jpg'));
width = size(im_d, 2);
height = size(im_d, 1);
channels = size(im_d, 3);

（1）定义该观察到的（失真的）图像的每个像素位置相对于图像中心的空间坐标。例如，由于该测试图像为4288×2872像素，因此左上像素坐标为（-2143.5，-1435.5）。

xs = ((1:width) - (width+1)/2);
ys = ((1:height) - (height+1)/2);
[X, Y] = meshgrid(xs,ys);

（2）将这些坐标转换为极坐标形式，这样我们就可以只操作径向分量（这里称为RHO）。我们还归一化并缩放径向坐标，使得未失真图像的中心到角落的距离最终归一化为1。

[THETA, RHO_d] = cart2pol(X, Y);
normFactor = RHO_d(1, 1); % normalize to corner distance 1 in distorted image
scaleFactor = polyval(inverseCoeffs, 1); % scale so corner distance will be 1 after distortion correction
RHO_d = RHO_d/normFactor*scaleFactor;

（3）注意：作为一个微妙的点，变量THETA和RHO_d对实际上以两种方式定义空间坐标：明确地和隐含地。它们在其值中定义了显式坐标，即其中（THETA（1，1），RHO（1，1））定义了图像左上角像素的角坐标和径向坐标。然而，它们也简单地通过2-D数组隐含地定义了一组坐标，这些数组具有自然的顺序和结构。即使我们改变了这两个数组的（1，1）项的值，它们仍然是每个数组的左上角项。点的显式坐标已更改，但隐式坐标保持不变。

现在，我们将测量到的失真应用于径向坐标，使得显式径向距离匹配所观察图像中的该点的径向距离。如上所述，观察到的图像中的该失真位置现在经由阵列中的隐式位置被绑定到图像阵列中的未失真位置。我们使用隐式阵列元素位置作为未失真图像的真实坐标，并且显式阵列值作为到失真图像中的点的映射以从中提取样本。

请注意，我们实际上还没有正向变换多项式，我们有Imatest返回的逆多项式。这可以通过拟合新的（逆的）多项式来反转，如提供的invert_distance_poly.m文件中所示。

forwardCoeffs = invert_distortion_poly(inverseCoeffs); 
RHO_u = polyval(forwardCoeffs, RHO_d); 
% Convert back to cartesian coordinates so get the (x,y) distorted sample points in image space 
[X_d, Y_d] = pol2cart(THETA, RHO_u*normFactor);

（4）我们现在有X_d，Y_d数组，其隐式坐标是未失真图像的坐标，并且其显式值指示与它们相关联的观察图像中的采样点。我们可以在interp 2（）函数中直接使用它们作为查询（采样）点。

% Re-sample the image at the corrected points using the interp2 function. Apply to each color
% channel independently, since interp2 only works on 2-d data (hence the name). 
im_u = zeros(height,width,channels); % pre-allocate space in memory
for c = 1:channels
   im_u(:,:,c) = interp2(X, Y, im_d(:,:,c), X_d, Y_d);
end

就是这样！现在我们可以看到我们劳动的未扭曲的成果。特别注意顶部和底部的直线。还要注意的是，在这个未失真图像的边缘周围有黑色区域-当然，原始图像中没有任何信息可以用来有意义地填充那里。

当然，除了测试卡图像之外，我们现在还可以恢复场景的失真。现在我们已经使用测试卡和Imatest来描述由摄像机系统本身引起的失真，我们可以在它拍摄的任何其他图像中消除这种失真。由于假定的直线建筑是一个非常常见的明显失真源，我们在科罗拉多州博尔德的办公楼的照片上展示了这一点，当天有漫射照明（即，昏暗）。

这些示例图像和MATLAB代码的更详细版本可在此处获得-distortion_correction_example. zip 5.4 MB

您可以在Imatest中自己测量图像中的失真，或使用distortion_correct_ex.m文件中提供的值。我们希望这篇文章有助于说明这个Imatest测量如何立即用于整合到您的管道中以改善您的图像。

Imatest径向几何模块（添加到Imatest 5.0，2017年8月）

如果您不想自己编写代码，可以使用Radial Geometry模块添加或纠正失真，该模块适用于单个图像或批量图像（使用最近运行的单个图像的设置）。全部详细信息（包括设置说明）在“径向几何体”说明中。

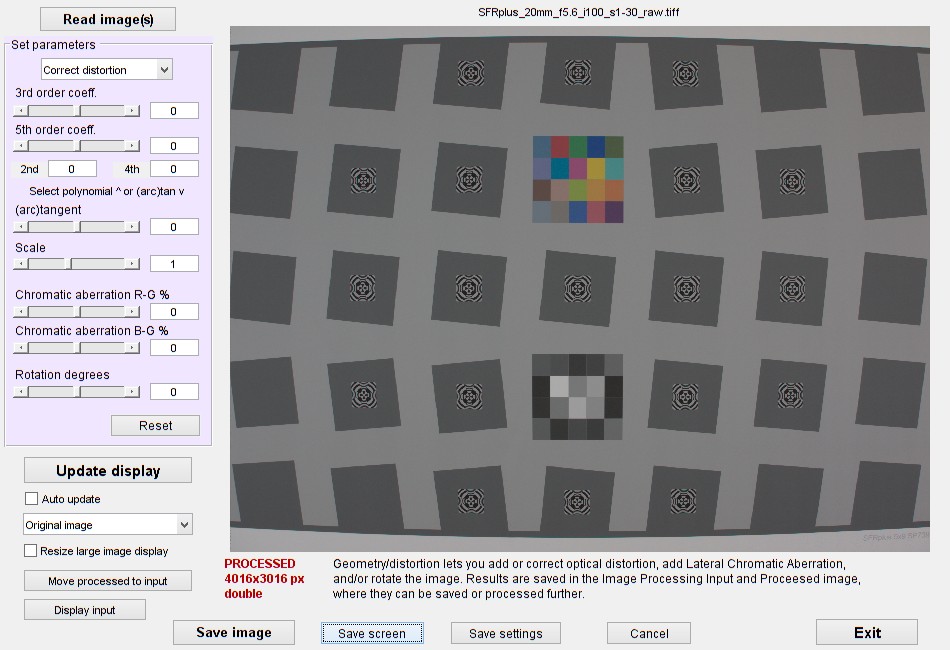
这是阅读SFRplus测试卡图像的失真图像后的输入窗口。

**径向几何体打开窗口。**
**该图像来自dcraw转换的图像（没有失真校正）。**

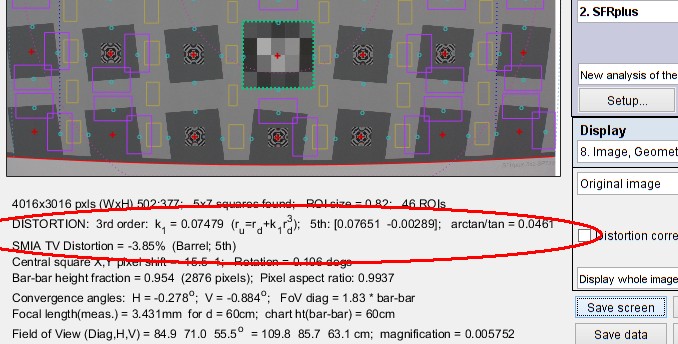
参数可从Imatest运行中获得：SFRplus如以下示例所示。

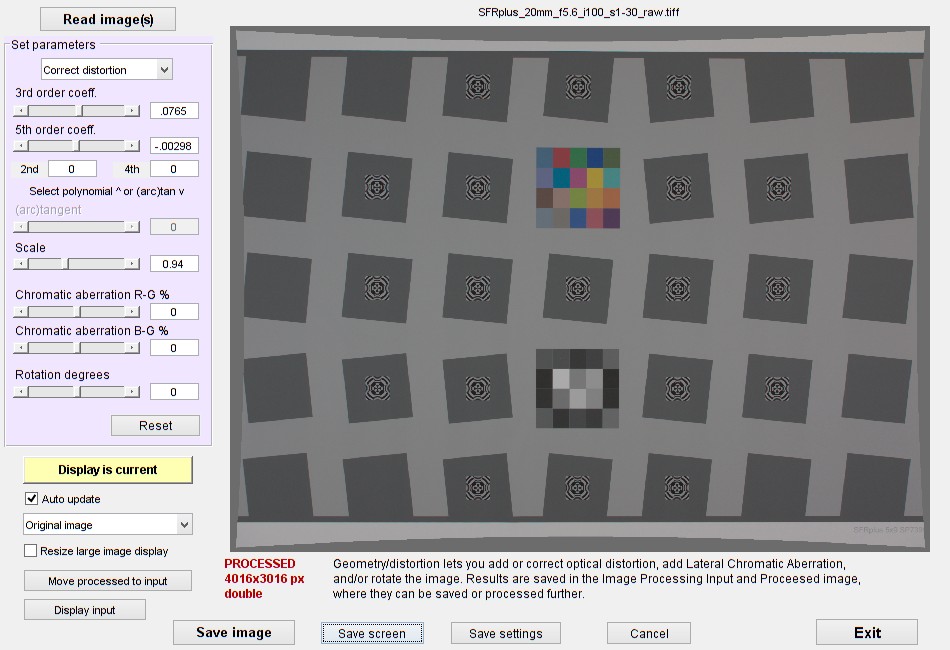
下面是修正后的结果。

联系我们

如果你有任何问题，欢迎与我们留言，也可邮件咨询： sales@colorspace.com.cn，分享您的看法或提出您的问题！

Was this helpful?

3 / 0

http://xzh.i3geek.com #imatest #几何畸变 #图像 #图像质量参数 #畸变 #畸变矫正

使用imatest软件辅助图像畸变校正