大多数人都熟悉音频这一概念。声音频率通过耳朵的变换感受为音节,所以放大器和扩音器等音频部件的工作特性通常用频率响应曲线表示。由于音频信号以时间参数描述为典型特征,因而电声设备对于信号的响应特性称为时间频率响应曲线。然而,模拟摄影和数字摄影图像都在二维空间上展开,可见借助于图像捕获数据的频率响应测量结果无法通过时间参数表示,成像系统或成像部件的工作特性必须改成以空间参数描述,称之为空间频率响应显得更为合理,测量结果也改称空间频率响应曲线。
根据 ISO 12233 电子静止图片照相机标准,空间频率响应定义为测量所得成像系统响应的幅值,通常以相对于输入空间频率的函数表示, 为简化叙述而缩写成SFR。据此,空间频率响应描述(绘制)为成像系统对于单位幅值输入信号的输出响应曲线,覆盖各种空间频率范围,且归一化处理后的空间频率响应在0频率处应该产生单位值,这意味着空间频率响应曲线在0频率处等于1。
理解成像系统的空间频率响应以及绘制成像系统的空间频率响应曲线离不开“归一化空间频率”这一概念,因为空间频率响应必须以归一化的空间频率为单位表示。所谓的归一化处理指空间频率与采样周期相乘得到积再除特定的距离尺度,空间频率和采样周期分别以每毫米周期数 cycles/mm 和 mm 为计量单位。
如前所述,成像部件或成像系统捕获的信号只能描述为空间域的形式。为了得到成像系统或部件对于原信号在空间域的频率响应特征,需要借助于傅里叶变换将成像信号转换到频率域;考虑到数字图像以离散数据描述的基本特点,大多采用基于快速傅里叶变换的算法实现从空间域到频率域的转换,根据计算结果即可得到原信号的频率分量。
由于描述图像的数据性质不同于音频信号那样的时间函数,且必须考虑到图像的二维描述特点,因而数字图像的空间频率响应分析需要执行二维的快速傅里叶变换。根据胶片的各向同性特点,这种成像介质沿任何方向的空间频率响应都是相同的,可见只要执行一维快速傅里叶变换即可,但镜头往往不具备各向同性特征。
二.调制传递函数
正确地理解调制传递函数这一概念需要对于“调制”两字的正确理解。根据 ISO 12233 给出的定义,调制传递函数中的“调制”两字指最大与最小信号水平之差除两者之和得到的商,若分别以 Sm和 Sn 标记成像系统或部件的最大和最小信号,则调制或调制值M 可以表示成下面这样的公式:
M=(Sm-Sn)/(Sm+Sn)
有了上述公式给出的对于调制(值)的定义,只需以输出调制(或频率)为分子、输入测试图的调制(或频率)为分母计算两者之商,即可得到成像系统的调制传递函数。
调制传递函数首先在光学成像领域提出,定义为光学传递函数 OTF 的模;而光学传递函数则定义为成像系统点扩散函数 PSF的二维傅里叶变换,通常以简称 MTF 表示。这种定义已使用了相当长的时间,用于描述图像(场景)信号在光学和摄影系统中的转移(传递)规律,并据此提出了多种测量方法,按周期信号、随机噪声和其他特征描述。
为了描述成像系统或部件再现被成像介质或对象细节的能力,人们往往以线扩散函数 LSF 和点扩散函数表示成像信号的变换特征,其中点扩散函数定义为成像系统线性化输出的归一化空间频率分布,来自理论上无限小点源的成像结果;线扩散函数与 PSF 类似,指成像系统线性化输出的归一化空间信号分布,来自理论上无限细线条的成像结果。
由于点扩散函数描述理论上无限小点源的成像特征,因而可以认为扩散行为具有各向同性特点,沿所有的方向都是均匀一致的。线扩散函数明显不同于点扩散函数,往往与线条类对象的边缘特征有关,因而涉及边缘扩散函数 ESF,意味着线扩散函数不满足各向同性条件。边缘扩散函数定义为归一化的空间信号分布,由成像系统的线性化输出得到,理论上产生于无限锐化边缘的成像结果。如果成像系统在等晕区域 (Isoplanatic Re- gion)区域内操作,且成像系统在其线性范围内运行,则线扩散函数等于边缘扩散函数的一阶导数。
一般来说,基于简单测量方法(未经校正)得到的结果称为空间频率响应,输入调制经过校正后的测量结果则称之为调制传递函数,两者并无原则区别。因此,只要不存在严格的限制条件,则可以认为空间频率响应与调制传递函数等价。
三.调制传递函数的累积效应
从结构角度看,图像由表示内容的“全貌”以及对图像可读性起加强作用的“细节”构成,分别对应于图像信号的低频和高频成分。图像质量主要由细节决定,可以认为图像细节与清晰度等价,适用于数字照相机和扫描仪捕获的数字图像。作为数字摄影或扫描的结果,图像对于阅读者或鉴赏者的吸引力在很大程度上取决于图像内容在二维平面上对于细节的积分。无论在胶片摄影或数字摄影年代,数量众多的摄影工作者耗费大量时间、精力和金钱购买设备,旨在获取清晰的图像。以扫描仪输入模拟原稿的印刷工作者同样如此。
成像系统或成像系统部件(例如照相机镜头、胶片、图像传感器、扫描仪和放大镜头等)的清晰度可以用称之为调制传递函数的参数描述,有时也称为空间频率响应。这里先给出对于调制传递函数的视觉解释,比如图 1 所示的测试图在成像系统部件作用下清晰度逐步降低的例子,说明调制传递函数的累积效应,与图像质量密切相关成像部件影响清晰度的累积效应。

图1的顶部按空间频率增加的次序设计成黑色与白色线条间隔的测试图,代表被复制对象的目标清晰度,对应于图像平面每毫米2到200线对数的分辨能力;图1给出的“图案”代表成像部件对清晰度的累积效应,包括镜头、胶片、镜头+ 胶片、图像捕获装置(扫描仪)和锐化算法,从已经公开发表的数据按计算机模型精确地推算而得。
四.调制传递函数测量
成像系统或部件以有限的空间分辨率为主要特征,为此需要测量成像系统或部件的分辨率;目前大多采用条状图案(例如图 1 顶部所示的原测试图)的测量方法。成像系统或部件再现原信号的能力或对于原信号的响应特征仅仅用空间分辨率描述是不够的,需要更综合性的指标。成像系统的性能更无法用单一的正弦波、频率和相位描述,需要更复杂的描述方式,这就需要调制传递函数。表面上看,引入调制传递函数导致问题的复杂化,但实际上变得更简单,只需一个量就可描述成像系统性能,比仅仅用空间分辨率描述更合理。
假定成像系统的输入信号可以分解成一系列的正弦波信号,这一问题通过傅里叶变换可得 到很好的解决;由于成像系统的作用,输入信号必然经过变换,形成不同于输入信号的输出信号;调制传递函数的测量目的归结为测量正弦波的幅值变化,认为成像系统对输入信号的作用是调制了原信号的幅值,先假定频率和相位不变,如图 2 所示。
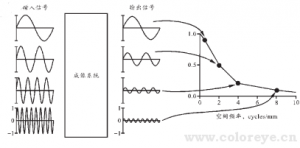
图 2 调制传递函数测量的基本概念
历史上曾经出现过各种空间频率响应或调制传递函数测量方法,例如模拟时代的小圆孔和 窄缝光孔测量法,以及数字时代的边缘梯度法和正弦图案测试图法等。此前的研究成果表明,边缘梯度法具有测试图简单和测试图像面积小的优点,缺点是测试图对齐的敏感性和噪声偏压; 正弦测试图法的主要优点归结为能够直接给出测量结果,但测量每一种频率分量的调制传递函数都需要准备相应的测试图,导致完成全部测量任务的时间太长。ISO 12233 定义的倾斜边缘空间频率响应或调制传递函数测量方法为简化测量过程带来了曙光,只需准备一幅图像(例如图 3 所示的水平和垂直倾斜边缘测试图)就可以测量成像系统或部件的空间频率响应或调制传递函数了。根据 ISO 12233 标准定义的倾斜边缘空间频率响应测量方法分析,倾斜边缘法的主要目的在于测量电子静止图片照相机(包括模拟电子照相机和数字 照相机)的空间分辨率,从而允许评价成像系统或部件的视觉分辨率、极限分辨率、频率混叠比、 空间频率响应和压缩人工膺(伪)像等。

应用倾斜边缘法时需要将边缘成像到探测器(传感器)上,测试图相对于水平(或垂直)方向略为倾斜,这样就可以从倾斜边缘测试图的垂直方向边缘得到探测器的水平空间频率响应。边缘梯度法不能直接利用照相机捕获的图像数据,必须借助于独立的仪器捕获数据,但倾斜边缘法却允许使用实际图像数据。由于倾斜边缘与水平方向不同的相位,因而图像传感器对每一行扫描线捕获的图像数据将给出不同的边缘扩散函数。尽管这些边缘扩散函数都是欠采样的,但可以通过将数据沿边缘“投射”的方法从数学上提高采样速率。
五.倾斜边缘法 SFR/MTF 测量
ISO 12233 标准采用的空间频率响应(测量) 算法基于数据分析,测量和分析所需的数据来自测试图的倾斜边缘过渡区域,建议测量时使用 ISO 12233 标准定义的测试图。倾斜边缘法建立在单一线扩散函数归一化离散傅里叶变换基础上, f 表示归一化的空间频率,而 LSF’W(j) 则代表来自倾斜边缘测试图选择区域 (兴趣区域) 的 Hamming 加窗、平均、中心定位和超级采样线扩散函数。倾斜边缘测量和分析算法涉及许多数据处理任务,执行 ISO 12233 附录 A 给出的以 C 语言代码表示的空间频率响应测量算法需要为离散傅里叶变换准备。
由 ISO 12233 定义的测量和分析数字照相机空间频率响应的步骤如下:
(1)围绕倾斜边缘定义由 m 行、每行 n 个像素组成的兴趣区域,作为数字照相机空间频率响应测量、分析和评价流程的输入;
(2)通过光电子转换函数 OECF 变换兴趣区域的图像数据,目的在于补偿数字照相机的光度测定响应,例如光度数据与灰度等级(色调等级) 数据间的非线性效应;
(3)倾斜边缘法处理彩色图像时需要在计算 SFR 前建立明度数据,为此必须计算 RGB 彩色图像的明度阵列,由每一个像素的红、绿、蓝数据的加权计算和得到明度数据,图 4 给出了以反射系数为例的数据转换顺序,假定兴趣区域以倾斜边缘为对称轴;
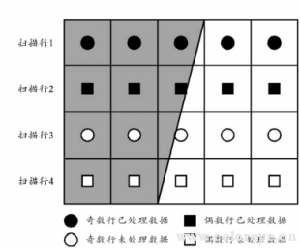
图 4 空间频率响应测量的数据转换
(4)借助于线性方程(线性化的图像数据)从明度数据阵列估计倾斜边缘的位置和方向,并计算垂直于倾斜边缘的一维离散形式的方向导数,例如通过差分法计算线性化图像数据的一阶(方向)导数。以中间差分为例,计算时要用到“- 1/2,+1/2”有限脉冲响应滤波器,这意味着当前处理像素X的一阶导数值等于其直接左面像素值的- 1/2 倍,再加上该像素右面之像素数值的 1/2 倍, 如图 5 所示计算过程;
图 5 边缘位置、方向估计与导数计算
(5)根据对原图像 RGB 值加权计算得到的明度数据计算每一数据行的质心,得到线扩散函数 LSF,该步骤在整个处理过程中占有特殊的地位;
(6)线性拟合处理,使线性方程拟合到质心位置,或者说计算明度数据行质心位置的最佳直线拟合,以确定倾斜边缘的准确位置;
(7)所有像素的图像数据“投射”到倾斜边缘方向,即沿每一条扫描线的图像数据如图 6 所示那样“投射”到兴趣区域顶部或底部的边缘方向,导致“数据包 / 数据堆栈”内不断地积累数据,像素宽度依次添加到“数据包”内;
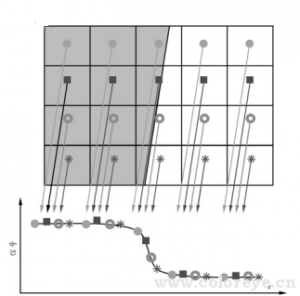
图6沿边缘“投射”数据
(8)组成一维的“超级采样”边缘扩散函数,完成 4 倍(默认过采样因子,允许由用户修改)的过采样操作,即以原图像采样周期的 1/4 作重新采样计算。上述过程通过形成超级采样边缘扩散函数提高采样速率,以降低空间频率响应测量/分析过程所受到的成像系统信号频率混叠的影响,图 7 和图 8 分别给出了同一测试对象边缘扩散函数和线条扩散函数的测量结果,以过采样因子4对 15×25 个像素组成的兴趣区域计算而得;
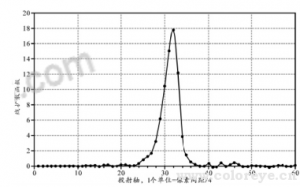
图 8 从边缘扩散函数推导而得的线扩散函数
(9)计算重新采样数组的边缘导数,并对计算结果应用 Hamming 加窗函数 / 数组;
Gibbs(吉布斯)现象:在计算傅里叶分布以及谐波数列叠加合成时,会产生尖锐而不连续的区间,如同方波的下降和上升那样,即所谓的吉布斯现象或吉布斯效应,这种现象产生的不仅与谐波叠加合成的数量有关,且谐波叠加变化的宽度随合成的谐波数量的增加而变窄。为了降低无限系列截断导致的吉布斯现象或吉布斯效应的影响,通常采取对线扩散函数应用 Hamming 窗的措施。
Hamming 窗:数字信号处理领域使用的窗函数之一,由美国数学家 Richard Hamming 提出,当 余弦曲线的上半部分取特殊的系数时,即形成 Hamming 窗,仍然具有余弦曲线上半部分(正值 部分)的基本形状,但加窗计算结果在类余弦曲 线中间产生细窄的脉冲。
(10)对Hamming 加窗数组执行离散形式的傅里叶变换(即快速富里叶变换),得到成像系统 或成像部件的空间频率响应,而成像系统或成像 部件的调制传递函数则可以借助于下式从空间频率响应推导出来;
式中的 FRtarget 代表测试图的频率响应,可通过多项式近似计算,因而成像系统或成像部件的空间频率响应SFR(f)与测试图频率响应的商是频率与频率相除的结果,计算起来没有困难。此外,修正由于三点差分(中间差分)导数计算过程引入的误差也是必须的,这可以采用纠正因子 MTFderiv的方法予以解决。
(11)对离散傅里叶变换的模作归一化处理, 作为数字照相机的空间频率响应测量 / 分析结果输出,用于绘制空间频率响应曲线和调制传递函数曲线,并用于评价成像系统或成像部件的分辨率和调制传递特性,也可用于成像系统或部件的性能比较。
Was this helpful?
13 / 3
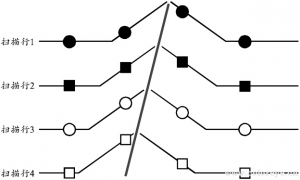
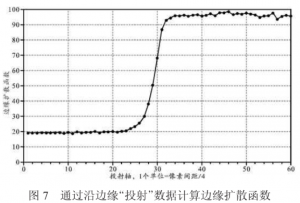
图1和图6漏掉啦…文章里找不到。